Corrected: Odds Ratio Walkthrough

In this walkthrough, we are going to learn more about odds ratios, how to calculate an odds ratio using a logistic regression model, and how to interpret the value of an odds ratio.

The formula for an odds ratio can be seen below.

odds ratio = \(\frac{probability \text{ of x} / (1 - probability \text{ of x})}{probability \text{ of y} / (1 - probability \text{ of y})}\)

\(\frac{probability \text{ of x}}{1 - probability \text{ of x}}\) can be thought of as the probability of a success over the probability of a failure. This is also known as the “odds” of a success. When you take the ratio of these two events. You get a ratio of odds, or an odds ratio!

Connection with logistic regresssion

The response for our logistic regression model is the log odds: \(ln(\frac{p}{1-p})\). In linear regression, \(\beta_k\) was the difference in the outcome associated with a 1-unit difference in \(X_k\) (or between a level and the reference level if X is categorical). Similarly, in logistic regression, it is the difference in the log-odds of the outcome associated with a 1-unit difference in \(X_k\).

It turns out that \(e^{\beta_k}\) is the odds ratio (OR) comparing the success of your response who differ by 1-unit in \(X_k\) when \(X_k\) is quantitative. We can show this below. Note that the odds of a success for a given logistic regression model are \(\frac{p}{1-p}\), and can be expressed as:

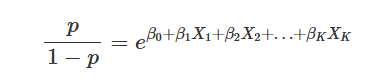
Thus, if we want to know how to odds change when we move over one unit, we can conduct an odds ratio where the numerator are the odds at X + 1, and the denominator are the odds at just X.

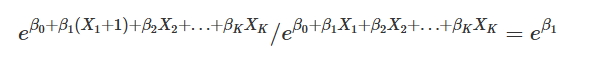
If the first predictor is instead categorical and we want the OR comparing the first non-reference level to the reference level, then we want the ratio of the odds at \(X_1 = 1\) to the odds of \(X_1 = 0\).

Example

Note: A success is defined as what level we are specifically interested in predicting. In R, this should be coded as the level 1.

Suppose we want to calculate the odds ratio for when the number of exclamation points an email increases. That is how much more likely is it that an email is span as we increase the number of exclamation points by 1.

Just like in linear regression, we are going to investigate what happens when increase the number of exclamation points by 1. Thus… we are going to calculate

odds ratio = \(\frac{probability\text{ of spam} | exclm + 1 / (1 - probability \text{ of spam} | exclm + 1)}{probability \text{ of spam} | exclm / (1 - probability \text{ of spam} | exclm)}\)

Calculation

We want to calculate how much more likely is it that an email is span as we increase the number of exclamation points by 1. Based on the math above, we know we can calculate this by taking \(e^{\hat{\beta_1}}\).

We can use the logistic regression model (created in class) below to find our estimated \(beta_1\).

\(\widehat{ln(\frac{p}{1-p})}\) = \(-1.911 - 0.168*\text{ex points}\)

Thus, our odds ratio is \(e^{-.168}\) = 0.845.

Interpretation

To best understand how to interpret the odds ratio, we need to understand the equation relative to the value of 1.

The odds ratio is the ratio of odds. So how can we interpret the actual value? Let’s interpret our odds ratio that we calculated above.

Interpretation: The odds ratio interpretation for number of exclamation points indicates that for every additional exclamation point increase, a spam email is .845 times as likely to be observed.

This is consistent with our visual exploration of these data. We observed more non-spam emails having more explamation points!