Checklist
– Keep up with Slack
– HW 5 (due Tuesday at 11:59)
– HW 6 has been released (due Tue 26th at 11:59; our last HW!)
– Quiz 11 (released Wednesday; due Sunday Nov 24)
– Don’t forget about the statistics experience (Due Dec 6th)
Anova
– Extension of difference in means
– \(Ho: \mu_1 = \mu_2 = \mu_3 = ... \mu_k\)
– \(Ha: \text{At least one population mean is different}\)
– F-statistic ~ \(F_\text{k-1, n-k}\)
Chi-square
– This is a test of independence between categorical data with any number of levels
– \(Ho: \text{x and y are independent}\)
– \(Ha: \text{x and y are not independent}\)
– chi-squared statistic \((\chi^2)\) ~ chi-square distribution \(\chi^2_\text{(r-1)*(c-1)}\)
Roadmap
– In unit 1 + Anova & Chi-square, we have done inferential statistics (taking a sample, and making claims about a larger population)
– In unit 2, we have used regression tools more descriptively (using data to make predictions, and interpret coefficients estimated from our data)
New topics:
– Logistic Regression
– Sampling methods
What we will do today
– This type of model is called a generalized linear model
![]()
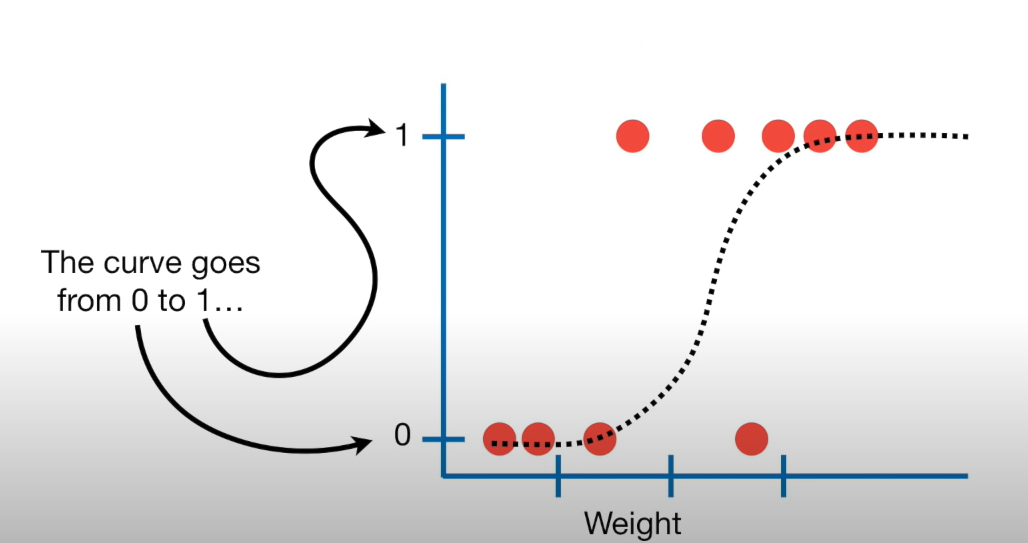
We want to fit an S curve (and not a straight line)…
where we model the probability of success as a function of explanatory a variable(s)
Terms
– Bernoulli Distribution
2 outcomes: Success (p) or Failure (1-p)
\(y_i\) ~ Bern(p)
What we can do is we can use our explanatory variable(s) to model p
Note: We use \(p_i\) for estimated probabilities
Probability
What values can probability take on?
Probability
Probabilities can take on the values of [0,1]…
Need: this means that we need to work with a model that constrains estimated probabilities (our response) to be on the correct scale [0,1]
The S curve
We can accomplish this using the following model
![]()
\(\widehat{ln(\frac{p}{1-p}})\) = \(\widehat{\beta_o} +\widehat{\beta}_1X1 + ....\)
Breaking down the model
\(ln(\frac{p}{1-p})\) is called the logit link function, and can take on the values from \(-\infty\) to \(\infty\)
\(ln(\frac{p}{1-p})\) represents the log odds of a success
p stands for probability
This logit link function restricts p to be between the values of [0,1]
Which is exactly what we want!
Breaking down the model
\(\widehat{ln(\frac{p}{1-p}}) = \widehat{\beta_o} +\widehat{\beta}_1X1 + ....\)
These are the coefficients that help us estimate the log odds, conditional on explanatory variable(s) in the model
The S curve
![]()
\(\widehat{ln(\frac{p}{1-p}}) = \widehat{\beta_o} +\widehat{\beta}_1X1 + ....\)
Currently, this model is modeling log odds… let’s go through and math out the model we need to use in order to estimate probabilities!
Math
\(\widehat{ln(\frac{p}{1-p}})\) = \(\widehat{\beta_o} +\widehat{\beta}_1X1 + ....\)
– How do we take the inverse of a natural log?
– Taking the inverse of the logit function will map arbitrary real values back to the range [0, 1]
So
\[\widehat{ln(\frac{p}{1-p}}) = \widehat{\beta_o} +\widehat{\beta}_1X1 + ....\]
– Lets take the inverse of the logit function
– Demo Together
Final Model
\[\hat{p} = \frac{e^{\widehat{\beta_o} + \widehat{\beta_1}X1 + ...}}{1 + e^{\widehat{\beta_o} + \widehat{\beta_1}X1 + ...}}\]
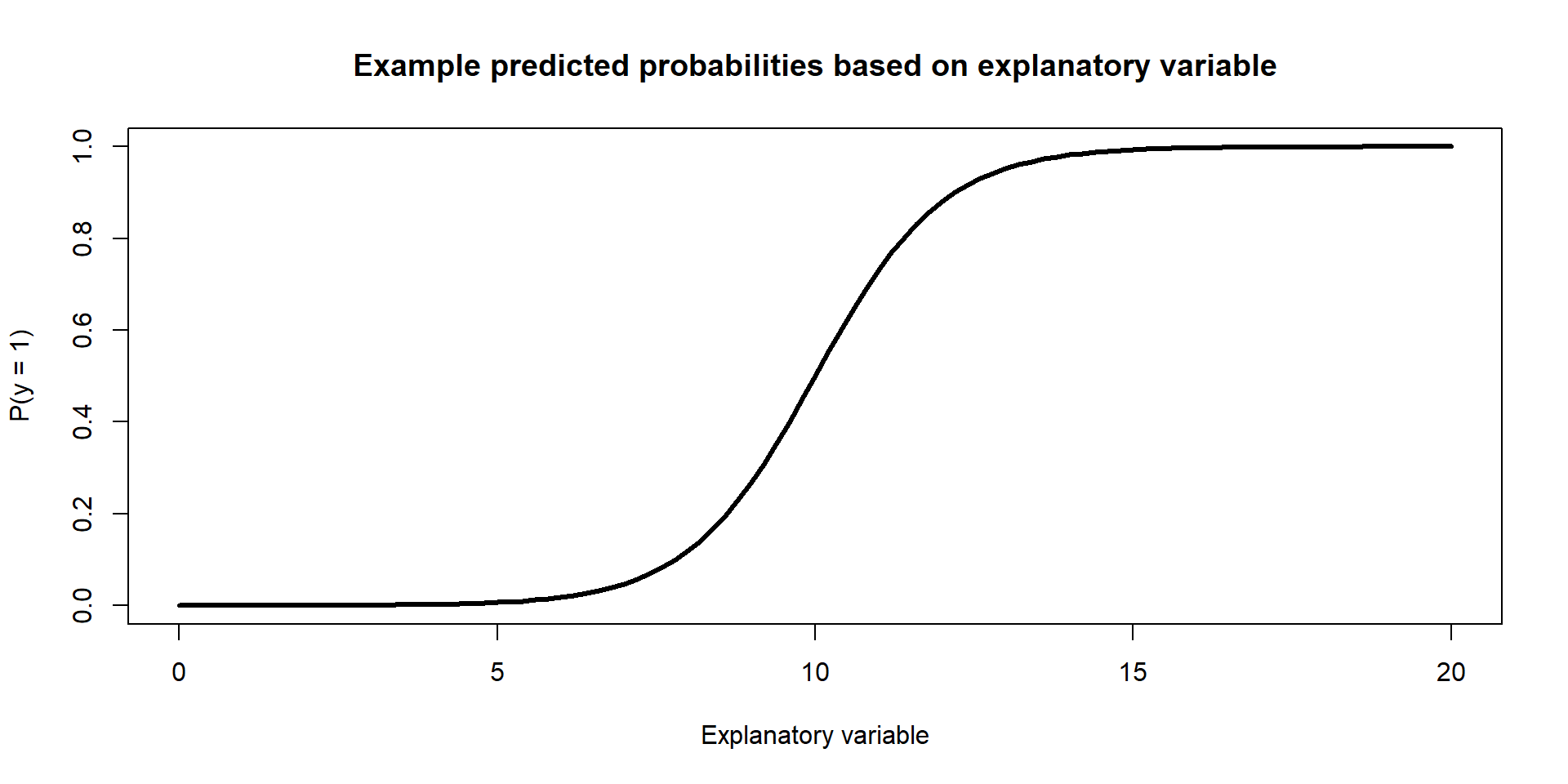
Example Figure:
![]()
Recap
With a categorical response variable, we use the logit link (logistic function) to calculate the log odds of a success
\(\widehat{ln(\frac{p}{1-p})}\) = \(\widehat{\beta_o} +\widehat{\beta}_1X1 + ....\)
We can use the same model to estimate the probability of a success
\[\hat{p} = \frac{e^{\widehat{\beta_o} + \widehat{\beta_1}X1 + ...}}{1 + e^{\widehat{\beta_o} + \widehat{\beta_1}X1 + ...}}\]
